Jido
미술의 투시원근법, 소실점과 어안 렌즈 본문
미술에서 투시원근법이라는 것이 있다.
또 컴퓨터의 3D 활용에서도 활용이 되기도 하고.
그리고 원근법 관련으로 소실점, 어안 렌즈(피시아이) 효과 등 용어들이 있는데,
실상 모두 3D 공간 상의 것들을 2D로 옮기기 위한 방편이라 볼 수 있다.
이에 개략적인 의미를 다루면 재미있을 것 같아서.
일단, 투시의 기본은 3D를 2D로 옮긴다는 것이다.
미술에서는 캔버스로, 컴퓨터에서는 화면으로.
TV나 카메라는 3D인 개체를 직접 찍으니 큰 고려를 하지 않는 부분이기는 하다.
그러면 3D를 2D로 어떻게 옮기나?
알아야 할 것을 순서대로.
1. 평행선은 무한으로 나아가면 한 점 즉 소실점에 모인다.

2. 다시 말하면, 동일한 각도를 갖는 평행선들은 모두 하나의 소실점만 갖는다.
캔버스로 옮기면, 아래와 같이 모든 평행선이 한 점으로 모이게 표현된다.

3. 캔버스 내 소실점의 위치는 선의 각도에 따라 정해진다.
눈으로부터 캔버스로 뻗은 점이 해당 각도를 공유하는 평행선의 소실점이다.
캔버스 가장자리로 뻗는 선의 각도는 시야각이며, 캔버스와 눈의 거리가 가까울수록 시야각은 더 커진다..

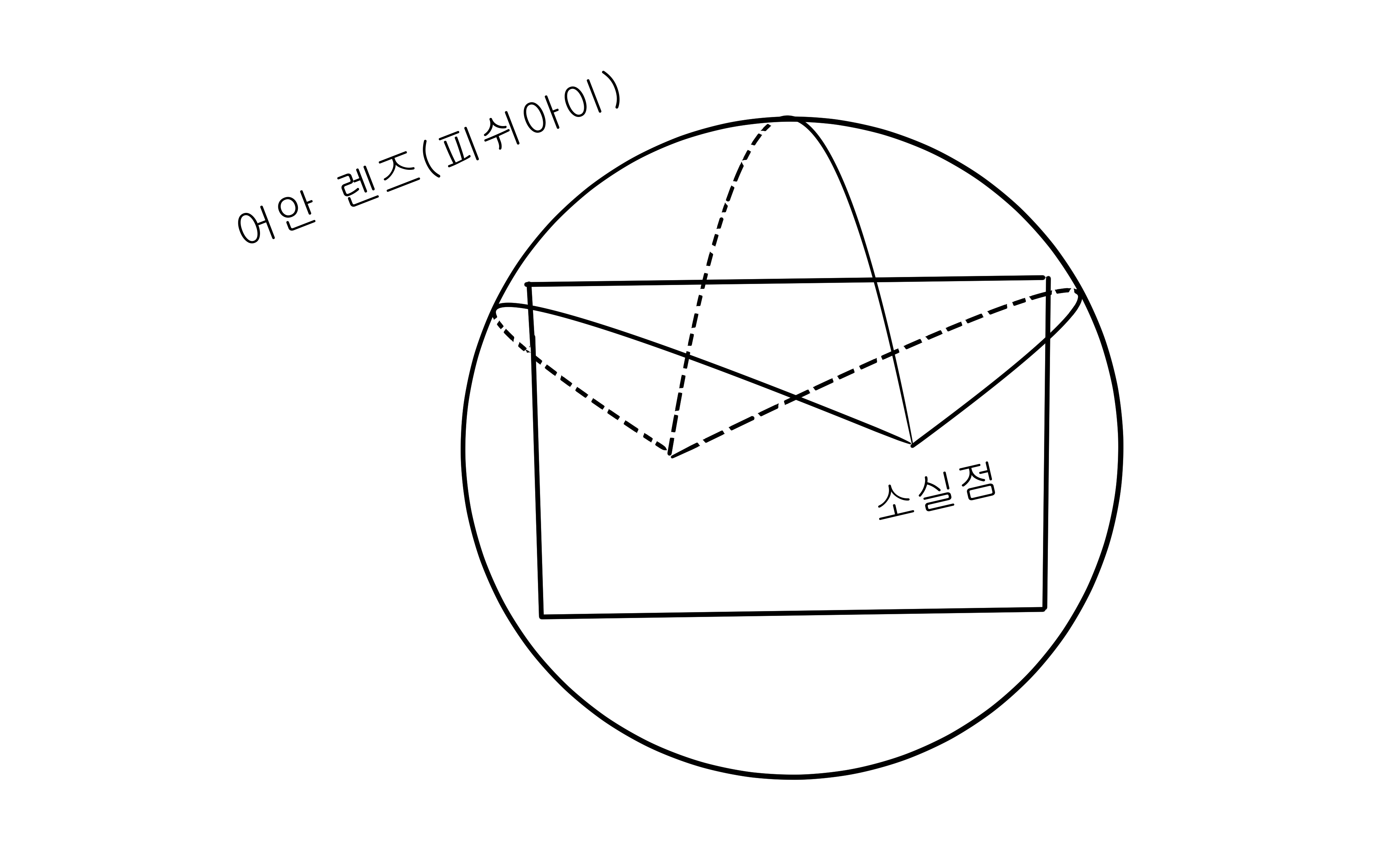
4. 어안 렌즈(피시아이)의 경우는 캔버스를 직선이 아닌 구로 본다.
따라서 평행선은 직선이 아닌 구를 따라 휘어지는 곡선이 된다.
구가 커지면 곡률이 낮아져서 평행선은 직선에 가까워지고, 구가 작아지면 높은 곡률로 선도 크게 휘어진다.
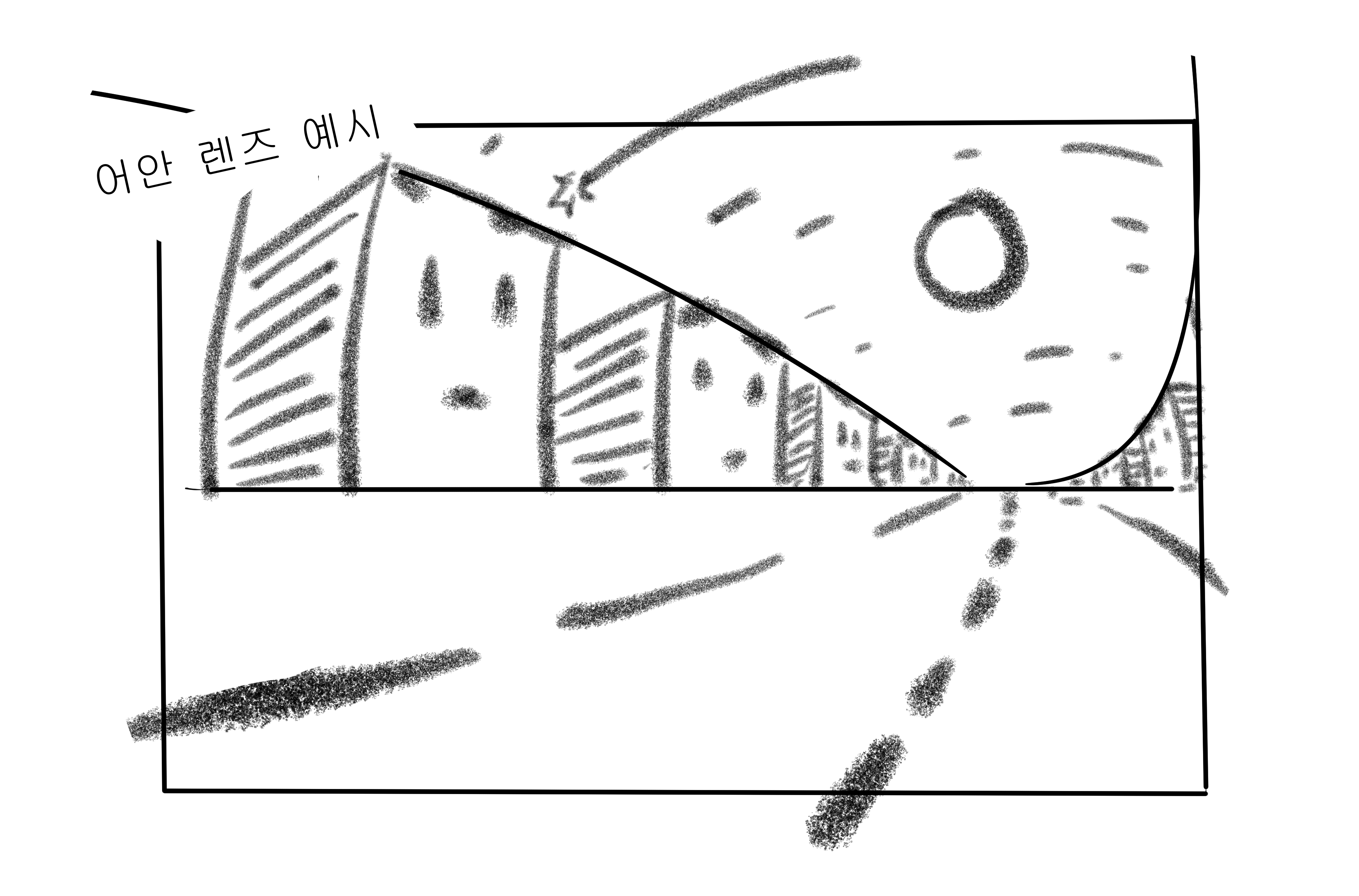
5. 어안 렌즈 효과를 이용하여 그림을 그리면 아래와 같다.
그림의 경우, 캔버스의 우측에 소실점이 위치히고
각각의 참조선이 되는 평행선은 곡선으로 표현이 된다.
이 정도가 아마 기초적인 내용 아닐까 싶다.
그러면 투시원근법은 3D를 2D로 옮기는 정확한 방법인가?
반은 맞고 반은 틀리다.
3에서도 보면 알 수 있다시피, 투시원근법은 기본적으로 관찰자의 위치를 고정한다.
즉, 실질 관찰자가 캔버스에서 그릴 때 가정한 정확한 위치에 있어야
의미가 있다는 말이다.
가령, 회화 작품은 화가의 위치를 상상하고 해당 위치에서 보면 더 많은 정보를 얻을 수 있다.
물론 디스플레이가 VR기기처럼 정확한 위치에 고정된다면,
더 정확한 표현이 가능하다 할 수 있다.
그리고 어안 렌즈의 경우는, 실질 우리가 물체를 보는 방식과는 많이 다르다.
렌즈를 하나 더 덧댄 경우로 볼 수 있으며, 실사와는 다른 어떤 효과를 위한 장치라 볼 수 있다.
물론 이 경우에도 오목한 디스플레이를 통해 보면 실제와 근사한 모습을 볼 수 있기는 하다.
그러면, 어안 렌즈는 왜 사용할까? 어떤 효과를 노릴까?
어안 렌즈 효과를 사용하는 가장 주된 이유는 공간의 왜곡이 주는 입체감 때문일 것이다.
거리에 따른 왜곡이 심해지면, 당연 입체감도 강하게 느낄 수 있다.
그리고 다른 이유는 어안 렌즈의 왜곡이 시야각을 키우는 역할을 하기 때문일 것이다.
앞서 3에서 관찰자(눈)가 캔버스와 가까워질수록 시야각이 커진다 했는데, 그 반대라 보면 된다.
넓은 시야각은 관찰자가 캔버스와 가까이 있다는 즉 현장감을 느끼게 한다.
반면 이런 행위는 높은 집중도를 요구하기에 피로감을 느낄 수 있는데,
3D 멀미 증상의 원인이 될 수도 있을 것이다.
즉 요약하면, 높은 입체감과 강한 현장감, 반면 높은 피로감.
공포 영화나 몰입도가 높은 게임에 주로 활용되지 않을까 싶다.
일러스트처럼 순간 시선을 끌 수 있는 장면을 연출하거나.
'겨겨울' 카테고리의 다른 글
| AI와 인간의 전쟁, 가능할까? (0) | 2024.05.07 |
|---|---|
| 중요 컴퓨터에서 롤 뱅가드 가동은 (0) | 2024.05.07 |
| 정권 인수인계 전에 벌어지는 일들 (0) | 2024.05.06 |
| 간단한 에어컨 원리 (0) | 2024.05.05 |
| 엣지 오브 투모로우의 갑옷 설정은 왜? (0) | 2024.05.04 |
